
IEC651 A-Weight Audio Filtering
|
|
|
|
|
|
|
IEC651A – A Processing Command for A-Weight Audio Filtering

Introduction
(View more DSP information or download the command module.)
This note describes an implementation of the IEC 651 standard [1] A-weight filter that compensates for frequency dependence in human hearing response. The filtering is packaged as a downloadable processing command, IEC651A [2]. This command runs on a Data Acquisition Processor in the embedded DAPL operating system environment. The problem of measuring apparent sound levels, the role of weighted filtering, and specific use of the IEC651A command for audio analysis are discussed.
Command Overview
The IEC651A command filters a data stream to account for the frequency sensitivity of human hearing in real time. Before moving on to the technical details, let's first briefly summarize the key properties of the IEC651A command.
- It is compatible with any Data Acquisition Processor product having a 32-bit onboard processor.
- It operates upon data streams captured at any sampling frequency in the range 200 to 50000 Hz. Of course, you will have to provide alias-free sampled data at whatever sampling frequency you specify.
- It completely automates filter design. Just tell it the sampling frequency, and it does all the rest.
- It can work in batch mode for data collection experiments, or in continuous operation.
- The number of channels you can analyze simultaneously and in real time depends only on Data Acquisition Processor processing capacity.
- It conforms to the IEC 651 A-weight reference filter model to within plus or minus 0.1 decibel (approximately 1%) from 10 Hz through 95% of the Nyquist sampling limit, at any sampling frequency. This improves on the standard-defined 0.7 dB tolerances for Level 0 instrumentation by almost an order of magnitude, making the command suitable for testing devices intended as Level 0 reference standards.
- Because the filter performance is based on numbers, not analog component tolerances, the same filter is equally applicable at all other application levels: Level 1 (general laboratory use), Level 2 (general field use) and Level 3 (gross field surveys).
- It requires no programming. Define the filtering operation using one line in the DAPL script that configures the data acquisition configuration.
- It is the easiest to use.
- Oh yes, the price is pretty good too.
Let's now move on to the technical details.
Accounting for Audibility of Sounds
The problem of measuring audibility of sounds is complicated by the nonlinearity of human hearing. The frequency dependence of human hearing is described by the Fletcher-Munson Curves.
" [The Fletcher-Munson Curve set] explains the non-linear response of the human ear, whereby very low and very high frequencies at a given physical intensity are perceived as softer than mid-range frequencies, with 3-4 kHz being the most sensitive frequency range." (Acoustics/Psychoacoustics Theory, Study Guide, Dr. Howard Fredrics, Brown University)
The Fletcher-Munson Curves describe sensitivity to pure tones, but in practice, many sound sources are anything but pure. The apparent loudness of a frequency mix is not necessarily a simple combination of responses to individual frequency bands. To make matters worse, the apparent loudness varies both with the level of the signal and the levels of background noise.
In an attempt to account for human hearing sensitivity in a standardized way so that measurement instruments can be compared, the International Electrotechnical Commission (IEC) issued Standard IEC 651. This standard identifies four application types (0 through 3) and three weighting curve characteristics (A, B and C).
"Owing to the complexity of operation of the human ear, it is not possible at present to design an objective noise measuring apparatus to give results which are absolutely comparable, for all types of noise, with those obtained by subjective methods. However, it is considered essential to standardize an apparatus by which sounds can be measured under closely defined conditions so that results obtained by users of such apparatus are always reproducible within stated tolerances." (IEC 651 - 1979)
The A-weighting characteristic is most widely used, and though originally intended for low-level sounds, it is commonly applied to higher sound levels as well.
Applying the A-Weighting Characteristic
For applying the A-weighting curve to a spectral power analysis, one common approach is to first measure the spectral power of a signal under test. The spectrum is partitioned into bands of increasing width, in a geometric sequence. Within each band, the relative contribution to the weighted audio power is adjusted by applying a correction factor based on tables given in the IEC standard. The weighted audio power is then the combination of the weighted contributions from each band.
A variation of this approach can be applied when using FFT techniques for the spectral power analysis. A weighting factor can be computed by integrating the A-weighting curve over the equally-sized frequency intervals spanned by the FFT. The resulting weight-factors are then applied term-by-term to the corresponding terms in the FFT power spectrum. This approach is somewhat awkward, however, because the weighting factors depend on the sampling interval and FFT size. And, of course, this only works in combination with FFT analysis.
An alternative approach is also supported by the IEC specification. The weighting curves are also described in the form of a linear low-order analog filter. Because of its linearity property, the filter adjusts the gain at each frequency but does not shift the signal energy from one frequency band to another, in this manner achieving the desired frequency-dependent weighting. If the original signal is passed through this filter, and then an FFT analysis is applied to the filtered signal, the FFT analysis yields results that are scaled according to the standard weighting curve. The power in the spectrum equals the apparent audio power as defined in the standard.
The IEC651A command is an implementation of the filtering method.
Digitizing an Analog World
An FFT analysis is applied to discrete-time samples of an audio signal. This is inconsistent with a weighting characteristic specified in terms of a continuous-time filter. Either the signal can be filtered first, in the continuous time domain, or the original signal can be sampled first and the filtering performed in the sampled data domain.
While it is possible to build an analog-world filter implementing the standard weighting curve, building a highly accurate one is not a trivial matter. The critical frequencies of the filter range from 26.6 Hz to 12200 Hz, almost three orders of magnitude. The range of component values, component tolerances, drift, parasitic effects, and even the physical packaging make the design and fabrication of the analog filter quite awkward. The difficulty of the task is indicated by the rather huge tolerances the standard allows — plus or minus 8% in response levels are acceptable for even the highest grade of laboratory filters (Level 0). This is not an attractive alternative.
Digital filtering is much more attractive. The cost of using large or small numbers is the same. The numerical computations can be performed in real time as the signal is digitized, with no need for separate filtering hardware. However, to make this happen, the right digital filter designs must be found. Until now, this alternative has had its own share of problems.
The problem isn't the capabilities of the digital filters. It is how to represent the behaviors of the analog-world filters in the digital-world filters so that the two correspond well in the frequency domain. The usual design techniques for mapping the properties of an analog filter into the equivalent digital filter (impulse-invariant mapping, Tustin's bilinear mapping, Schneider's quadratic mapping, Yule-Walker least-squares fitting, direct rational approximation, etc.) all have limitations. Some techniques work well over part of the frequency range, but then fall apart in the rest of the range. Other methods deliver designs that are accurate but unstable, and therefore useless for real-time filtering.
To understand how some of the difficulties arise, consider for example the simplest of digital filters, a first-order stage with z-domain characteristic
Y a + bz
--- = --------
U 1 + cz
The frequency response of this expression is obtained by substituting z = e(j w T) where w is frequency expressed in radians per second and T is the sampling time. The nonlinear term e(j w T) is dependent on the sampling time interval T. Change the sampling time, T, and the filter response changes, in a nonlinear manner. Change the sampling time, and the entire filter stage must be re-designed to obtain an equivalent frequency response at the new sampling rate. The problem just gets more complicated for the case of the more complex A-weight filters.
So what is the solution to this? Simple — you get somebody else to do the design work. The IEC651A command from Microstar Laboratories provides a complete, integrated, and extremely efficient solution. It combines the best parts of several design methods and integrates them into one automated process.
Using the IEC651A Command
The following example shows a complete DAPL script for a data acquisition configuration. This configuration sends all of the A-weighted data to the PC for logging to a disk. (A PC application program takes care of all of the PC-side data management.)
// Configure the sampler for one analog channel
// and 44 kHz sampling rate
RESET
CONSTANT SAMPLING = 44000
IDEFINE ACQUIRE 1
SET IP0 S0
TIME 22.75 ; = 44 kHz rate
END
// Apply processing: IEC651A filter
PDEF AWEIGHT
IEC651A(IPIPE0,SAMPLING,$BINOUT)
END
START
The input sampling procedure configured by the IDEFINE command group defines one single-ended analog data channel. Samples are captured at 22.75 microsecond intervals, which corresponds to a 44 kHz rate. The processing procedure configures the A-weight filtering for operation at the 44 kHz sampling rate. When the START command is executed, the sampling and processing configurations work together, applying A-weight filtering to the data samples from the input sample pipe, placing the computed results into the $BINOUT binary data channel for transfer to the PC host.
Does it really work? The following configuration substitutes an artificially-generated broad-band noise signal for the signal samples, then computes the FFT spectra of the original noise signal and the filtered version so that they can be compared.
// IEC A-weight Filtering Demo
RESET
CONSTANT SAMPLING = 22500
PIPE POUT, PIN, PR1, PR2
PIPES SIGSPECT, FILTSPECT, AVSSPECT, AVFSPECT
PDEF AWEIGHT
// No external samples,
// substitute white noise signal
RANDOM(0,7171,PR1)
RANDOM(0,81666,PR2)
PIN = (PR1-PR2)/2
// Apply the A-weight filtering
IEC651A(PIN,22500,POUT)
// Analyze results and send to PC host
FFT32(5,9,0,PIN,SIGSPECT)
FFT32(5,9,0,POUT,FILTSPECT)
BAVERAGE(SIGSPECT,256,64,AVSSPECT)
BAVERAGE(FILTSPECT,256,64,AVFSPECT)
MERGE(AVSSPECT,AVFSPECT,$BINOUT)
END
START
The sampling rate of 22500 Hz yields a Nyquist limit of 11250 Hz in the frequency spectrum, so each 256-term block of FFT spans from 0 through 11250 Hz, roughly half of the audio range. The following plot displays the input and output signal spectra. You can download a copy of the command module and verify these results for yourself.
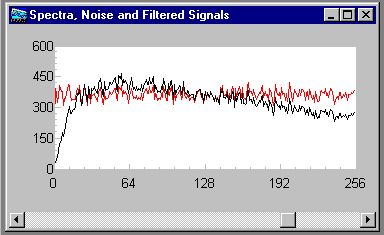
The two spectral plots are obtained by passing the pre-filter and post-filter data streams through FFT processing. The results of analyzing randomized data streams are very noisy, so groups of 64 spectra are averaged.
The results clearly show the effects of the A-weight filter. From a zero-of-transmission at frequency zero, the filter response increases. At 1000 Hz the original spectrum and the filtered spectrum track exactly. This reflects the fact that the A-weight filter characteristic is normalized with 0 dB at 1000 Hz. At approximately 6000 Hz, near the middle of the spectrum plot, there is another crossing of the 0 dB gain level. From there on through the end of the spectrum there is a gradual rolloff. Between 2000 Hz to 4000 Hz there is a small but distinct positive gain. All of these features correspond to the properties of the standard A-weighting curve.
Conclusions
A-weighted spectrum analysis using a digital filter has many advantages but requires an uncorrupted digitized signal and a good filter design. Thanks to the IEC651A processing command, the problems of obtaining the good digital filter design are solved. Obtaining a good digitized signal is still a challenge, but no different for A-weight filtering than any other sampled data application.
While not specifically addressing the possibilities, this technical note has suggested that other features built into the DAPL operating system complement the IEC651A filter processing. Among these,
- real-time FFT operations,
- data averaging,
- other kinds of frequency-selective filtering,
- direct control of the data acquisition process.
The DAPL system is powerful in its own right, but the IEC651A filtering command extends this power, making high precision audio spectrum analysis easy and cost effective.